Transient Tracers and Tracer Ages

Transient Tracers
Measurements of chemical tracers with time varying sources or sinks ("transient tracers") can provide information on transport time scales. From measurements of these tracers it is possible to define various timescales (``tracer ages''). There are several different classes of transient tracers, and different methods for calculating tracer ages.
One class of tracers are conserved tracers with monotonically increasing (or decreasing) surface concentrations. Examples of such "chronological tracers" in the stratosphere include carbon dioxide CO₂ and sulfur hexafluoride (SF₆), which both have increasing tropospheric concentrations and extremely long stratospheric lifetimes. In oceans, lakes, and groundwater suitable chronological tracers include chlorofluorocarbons (e.g., CFC-11, CFC-12, and CFC-113) and SF₆. The atmospheric concentration of these chemicals all increased with time until (at least) the early 1990s (see figure below), and they are also conserved in the above water bodies.
[Click on highlighted images for larger view.]

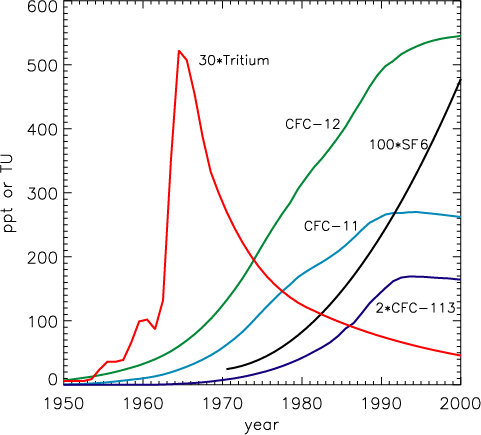
Time series of atmospheric concentrations, for background air in northern hemisphere troposphere, of CFC-11, CFC-12, CFC-113 and SF₆. Also shown is time series of tritium in North Atlantic Ocean surface waters.

From the above "chronological" tracers it is possible to a define a tracer age as the elapsed time since the surface concentration was equal to the interior concentration, i.e.,

c(t) = c₀(t-τ),

where c₀ is the surface tracer concentration, and c the interior concentration. This is illustrated below where stratospheric CO₂ measurements are compared with tropospheric time series, and a lag time (or "age") of 4-5 yrs is determined.

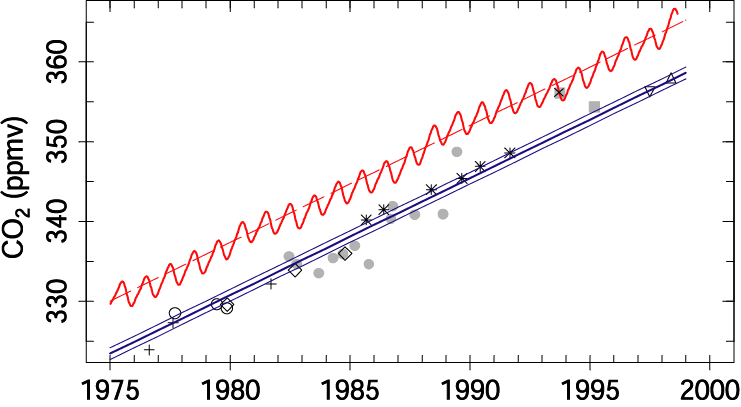
Variation of observed stratospheric CO₂ with time for balloon measurements in NH middle latitudes. Symbols correspond to average values in region above 20-25 km where there are weak vertical gradients. The shaded curve represents the stratospheric boundary condition for CO₂, and the long dashed line is a linear fit to this boundary condition. The thick solid line is this fit delayed by 4.5 year, and the dashed lines correspond to delays of 4 and 5 years. (From Andrews et al. [2001].)}

Stratospheric measurements of CO₂ and SF₆ have been used to determine the age of stratospheric air. In oceans, lakes, and groundwater tracer concentration ages are routinely calculated from CFC measurements (these ages are often called "pCFC ages"), see articles by Fine and Plummer and Busenberg for reviews of ocean and groundwater research, respectively.

The ratio of certain CFCs has also increased monotonically (e.g., CFC11/CFC12 ratio until 1980) and this ratio can be used to define a "ratio" age in a manner analogous to the above concentration age, i.e., the ratio age is the elapsed time since the ratio of two tracers at the surface was equal to the interior ratio.

Another class of transient tracers are those whose mixing ratios vary periodically. One can define an age, or "phase lag time", from the lag time of a maximum (or minimum) in the time series at an interior location from that at the boundary. Two such tracers in the stratosphere are CO₂ and H₂O, both which have annual cycles. The annual cycle in stratospheric CO₂ is forced by the annual cycle in surface CO₂, the result of seasonal variations in biota sources and sinks. The cycle in H₂O is forced by the annual cycle in tropical tropopause temperatures which regulates (via dehydration) the values of H₂O entering the stratosphere. The vertical propagation of the annual cycle in H₂O in the tropical stratosphere is shown below, from which a phase lag time of around 1 yr at 28 km can be determined.

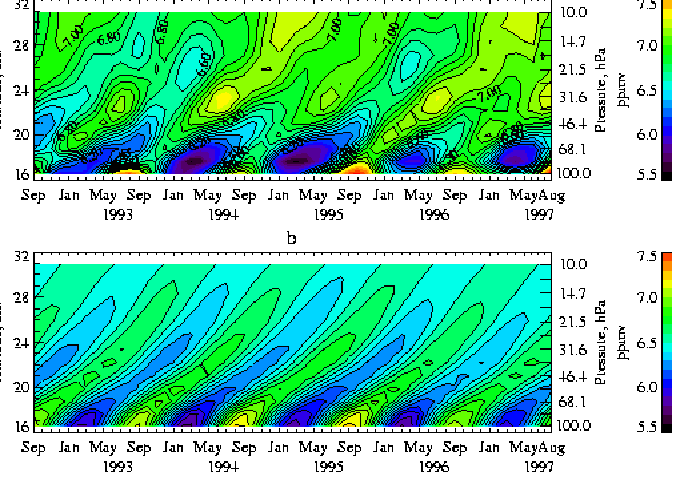
Height-time variation of HALOE measurements of water vapor in the tropical stratosphere. From Mote et al. (1998).

Another class of transient tracers measured in oceans, lakes, and groundwater are those undergoing radioactive decay, e.g., tritium, argon, natural radiocarbon. If the surface concentration is approximately constant in space and time then a ``radioactive" tracer age can be defined as

τ = λ^-1ln (c₀/c),

where c₀ is the surface tracer concentration, c the interior concentration and λ the tracer decay constant. As there are significant temporal variations in the surface concentration of tritium, due to atmospheric bomb testing in the mid-1960s (see plot above), a modified form has to be used to define an age from tritium and its daughter product helium-3:

τ = λ^-1 ln { (³H + ³He) / ³H },

where ³H is trituim concentration, ³He is the helium-3 that has come from tritium decay, and λ is the decay constant of tritium. Tritium-helium ages have been calculated from measurements in oceans, lakes, and groundwater, see, e.g., WHOI-HIL webpage.

Relationship among tracer ages
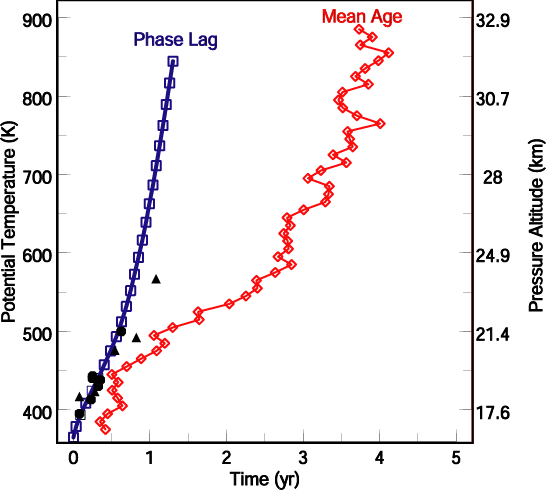
In general, the ages derived from different transient tracers differ. For example, the plot below compares ages in the tropical stratosphere derived from a chronological tracer (CO₂) and from a periodic tracer (H₂O). The phase lag time is younger than the concentration age throughout the stratosphere with large differences in the upper stratosphere.

Vertical profiles of "mean age", dervied from CO₂ measurements, and "phase lag" time, derived from H₂O measurements, in the tropical stratosphere.

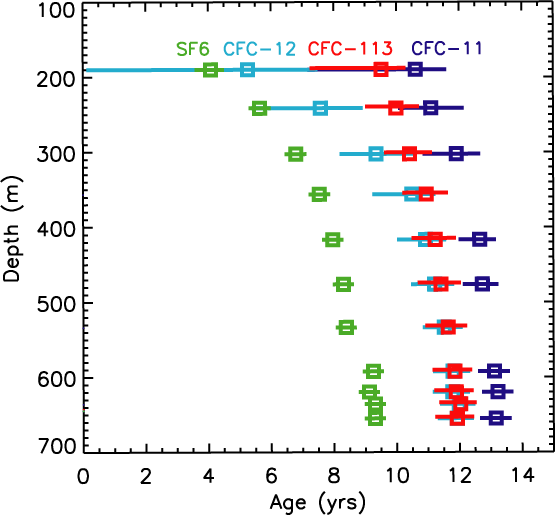
The ages from tracers differ even for the same class of tracers. This is illustrated below for tracer ages derived from measurements of CFCs and SF₆ in Lake Issyk-Kul.

Vertical profiles of tracer ages derived from measuements in Lake Issyk-Kul (Vollmer et al. 2000).

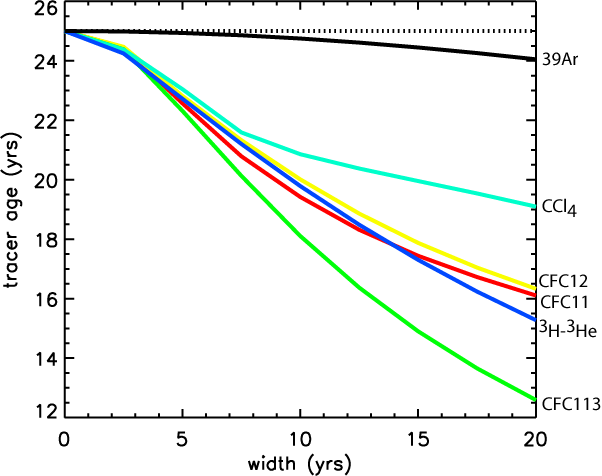
The differences between the different tracer ages are a result of mixing and the existence of a distribution of transit times. Each tracer, because of its different boundary condition or decay rate, weighs features of the distribution differently and so in general different tracers yield different ages. The variations of several different tracer ages with width Δ, for mean age Γ = 25 yrs, is shown below. For Δ=0 all tracer ages equal the mean age, but for Δ > 0 the tracer ages are younger than the mean age and different tracers yield different ages. The larger Δ, corresponding to more mixing, the larger the difference between tracer ages.

Variation of tracer age (in 1991) with width Δ for Γ=25 yrs, for several halocarbons (CFC-11, CFC-12, CFC-113 and CCl₄) concentration ages, and tritium-helium and argon radioactive tracer ages. Note that y-axes cover only 10 to 26 yrs.

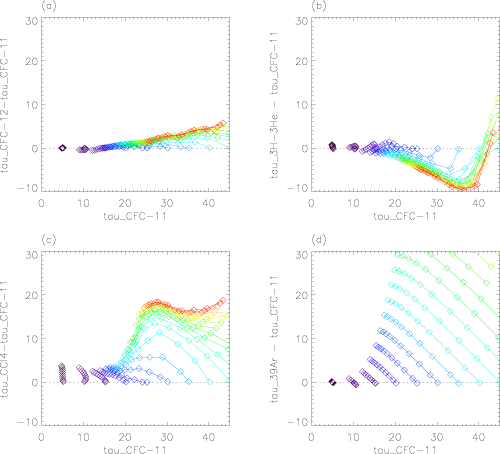
The differences between the tracer ages shown above can be understood in terms of the differing growth rates of the tracers (see Transit Time Distributions Section). For the 20-yr period before 1991 CFC-113 had the fastest growth rate, CCl₄ the slowest, and CFC-11 and CFC-12 had similar growth rates. Thus CFC-113 age < CFC-11 age < CFC-12 age < CCl₄ age. The relationship of different tracer ages with CFC-11 ages for a wide range of Γ and Δ is shown below. These plots show that the age-age relationships depend on both the tracers and the TTD. For more discussion of relationships among tracer ages see Waugh et al., JGR, 2003 .

Relationships between CFC12, tritium-helium, CCl₄, and argon ages with CFC11 age (y-axis shows the difference in the two tracer ages). The different curves correspond to different mean ages (Γ = 5, 10, ..., 100 yrs), and symbols to the different widths (Δ varies from 0 to Γ in 10 equal intervals). The symbols on the horizontal dotted line correspond to Δ = 0 whereas those at the end of the curves correspond to Δ = \Γ.

The plots above show that there can be significant differences between ages derived from different tracers. While this complicates the interpretation of single age measurements, it does raise the possibility of using tracer ages in combination to constrain the TTD. In particular ages from two tracers can be used to determine the first two moments of the TTD (i.e. the mean age and width). This approach has been used to constrain the TTDs in Lake Issyk-Kul and in the subpolar North Atlantic Ocean .

Back to Transit Times in Geophysical Flows.